刘英涛:达观数据推荐算法工程师,负责达观数据个性化推荐系统的研发与优化。
XGBoost的全称是 eXtremeGradient Boosting,2014年2月诞生的专注于梯度提升算法的机器学习函数库,作者为华盛顿大学研究机器学习的大牛——陈天奇。他在研究中深深的体会到现有库的计算速度和精度问题,为此而着手搭建完成 xgboost 项目。xgboost问世后,因其优良的学习效果以及高效的训练速度而获得广泛的关注,并在各种算法大赛上大放光彩。
1.CART
CART(回归树, regressiontree)是xgboost最基本的组成部分。其根据训练特征及训练数据构建分类树,判定每条数据的预测结果。其中构建树使用gini指数计算增益,即进行构建树的特征选取,gini指数公式如式(1), gini指数计算增益公式如式(2):
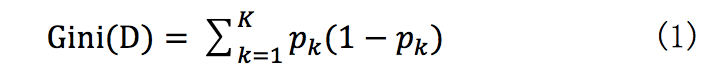
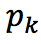 表示数据集中类别的概率,表示类别个数。
表示数据集中类别的概率,表示类别个数。
注:此处图的表示分类类别。
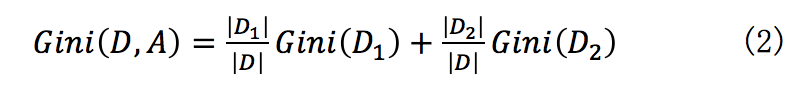
D表示整个数据集,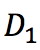 和
和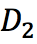 分别表示数据集中特征为的数据集和特征非的数据集,
分别表示数据集中特征为的数据集和特征非的数据集,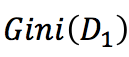 表示特征为的数据集的gini指数。
表示特征为的数据集的gini指数。
以是否打网球为例(只是举个栗子):
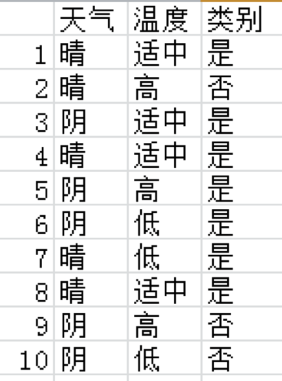
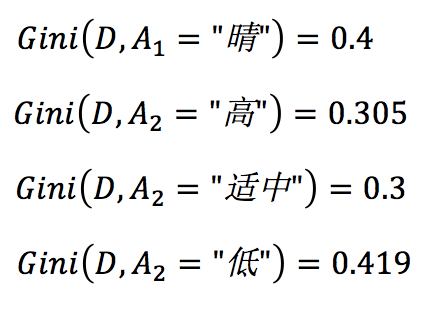
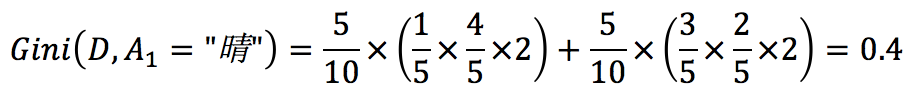
其中,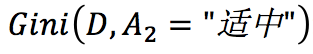 最小,所以构造树首先使用温度适中。然后分别在左右子树中查找构造树的下一个条件。
最小,所以构造树首先使用温度适中。然后分别在左右子树中查找构造树的下一个条件。
本例中,使用温度适中拆分后,是子树刚好类别全为是,即温度适中时去打网球的概率为1。
2.Boostingtree
一个CART往往过于简单,并不能有效地做出预测,为此,采用更进一步的模型boosting tree,利用多棵树来进行组合预测。具体算法如下:
输入:训练集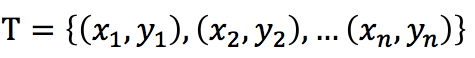
输出:提升树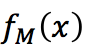
步骤:
(1)初始化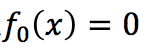
(2) 对m=1,2,3……M
a)计算残差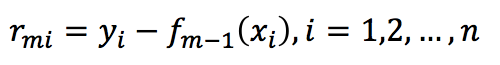
b)拟合残差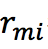 学习一个回归树,得到
学习一个回归树,得到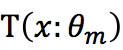
c)更新 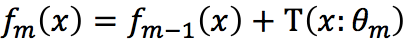
(3)得到回归提升树: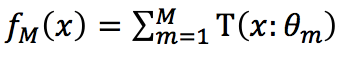
例子详见后面代码部分。
3.xgboost
首先,定义一个目标函数:
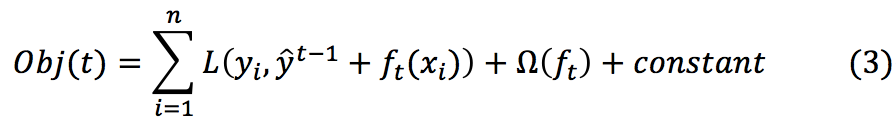
constant为一个常数,正则项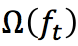 如下,
如下,
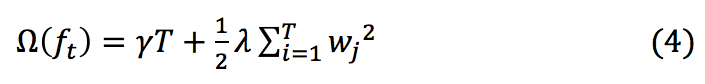
其中,T表示叶子节点数,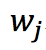 表示第j个叶子节点的权重。
表示第j个叶子节点的权重。
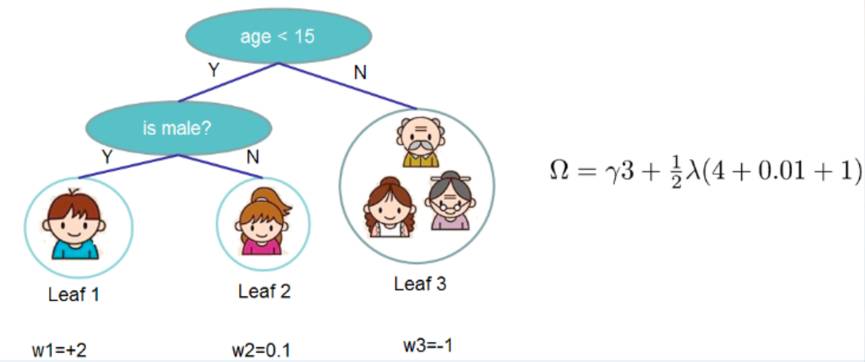
例如下图,叶子节点数为3,每个叶子节点的权重分别为2,0.1,-1,正则项计算见图:
利用泰勒展开式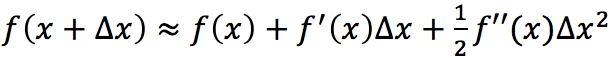 ,对式(3)进行展开:
,对式(3)进行展开:
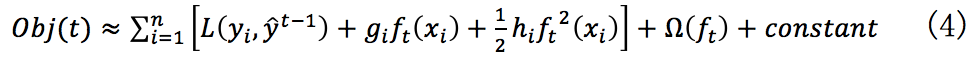
其中,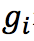 表示
表示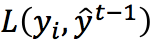 对
对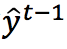 的一阶导数,
的一阶导数,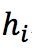 表示
表示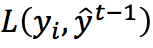 对
对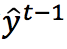 的二阶导数。
的二阶导数。
 为真实值与前一个函数计算所得残差是已知的(我们都是在已知前一个树的情况下计算下一颗树的),同时,在同一个叶子节点上的数的函数值是相同的,可以做合并,于是:
为真实值与前一个函数计算所得残差是已知的(我们都是在已知前一个树的情况下计算下一颗树的),同时,在同一个叶子节点上的数的函数值是相同的,可以做合并,于是:
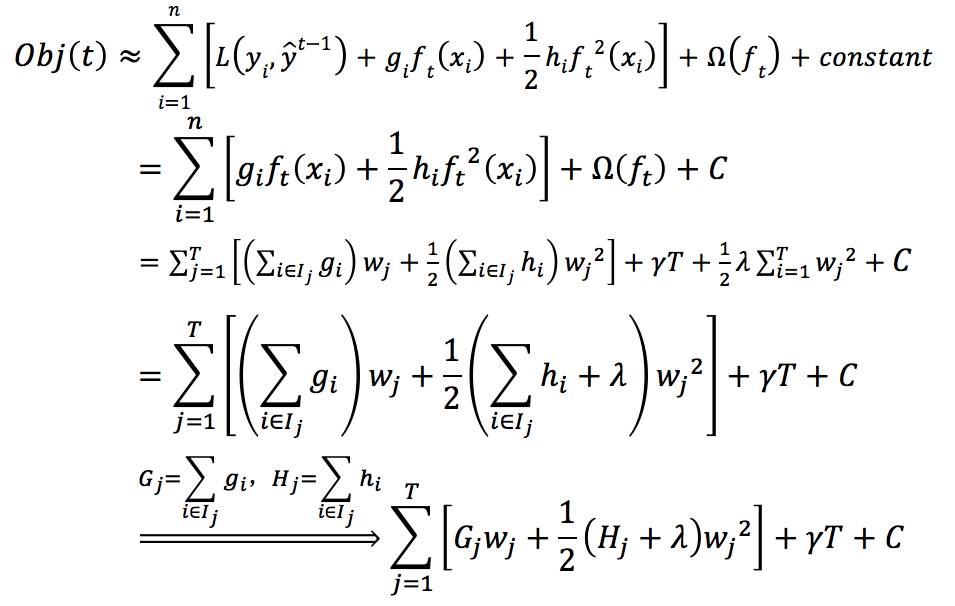
通过对求导等于0,可以得到

将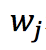 带入得目标函数的简化公式如下:
带入得目标函数的简化公式如下:
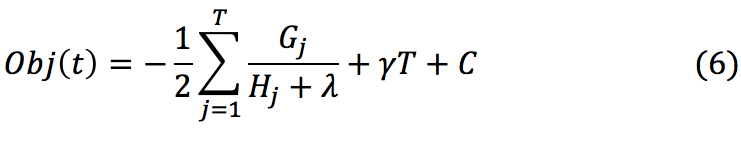
目标函数简化后,可以看到xgboost的目标函数是可以自定义的,计算时只是用到了它的一阶导和二阶导。得到简化公式后,下一步针对选择的特征计算其所带来的增益,从而选取合适的分裂特征。
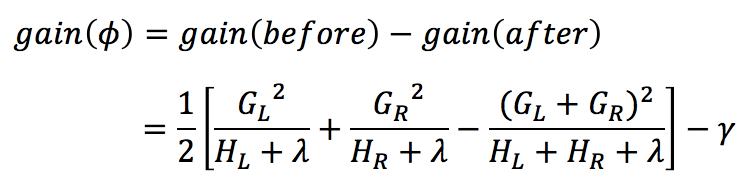
提升树例子代码:
# !/usr/bin/env python
# -*- coding: utf-8 -*-
# 目标函数为真实值与预测值的差的平方和
import math
# 数据集,只包含两列
test_list = [[1,5.56], [2,5.7], [3,5.81], [4,6.4], [5,6.8],
[6,7.05], [7,7.9], [8,8.7], [9,9],[10,9.05]]
step = 1 #eta
# 起始拆分点
init = 1.5
# 最大拆分次数
max_times = 10
# 允许的最大误差
threshold = 1.0e-3
def train_loss(t_list):
sum = 0
for fea in t_list:
sum += fea[1]
avg = sum * 1.0 /len(t_list)
sum_pow = 0
for fea in t_list:
sum_pow +=math.pow((fea[1]-avg), 2)
return sum_pow, avg
def boosting(data_list):
ret_dict = {}
split_num = init
while split_num <data_list[-1][0]:
pos = 0
for idx, data inenumerate(data_list):
if data[0]> split_num:
pos = idx
break
if pos > 0:
l_train_loss,l_avg = train_loss(data_list[:pos])
r_train_loss,r_avg = train_loss(data_list[pos:])
ret_dict[split_num] = [pos,l_train_loss+r_train_loss, l_avg, r_avg]
split_num += step
return ret_dict
def main():
ret_list = []
data_list =sorted(test_list, key=lambda x:x[0])
time_num = 0
while True:
time_num += 1
print ‘beforesplit:’,data_list
ret_dict =boosting(data_list)
t_list =sorted(ret_dict.items(), key=lambda x:x[1][1])
print ‘splitnode:’,t_list[0]
ret_list.append([t_list[0][0], t_list[0][1][1]])
if ret_list[-1][1]< threshold or time_num > max_times:
break
for idx, data inenumerate(data_list):
if idx <t_list[0][1][0]:
data[1] -=t_list[0][1][2]
else:
data[1] -=t_list[0][1][3]
print ‘after split:’,data_list
print ‘split node andloss:’
print’n’.join([“%st%s” %(str(data[0]), str(data[1])) for data inret_list])
if __name__ == ‘__main__’:
main()